パンダでもわかる量子プログラミング( IBM Quantum Composer)

わたしと一緒にIBM Quantum Learning で量子プログラミングをしてみましょう!今回は、量子プログラミング環境と、まずは実行するという事がミッションです。
1.IBMの量子コンピュータを使うためにはIBMidの登録をします。 https://learning.quantum.ibm.com/
アカウントを登録してログインできれば以下になります。
コースやチュートリアルもありますので、「量子情報の基礎」や「量子安全暗号の実践的な入門」はおすすめです。
早速プログラミングしましょう!
Quantum Composerの画面はこの様な感じです。
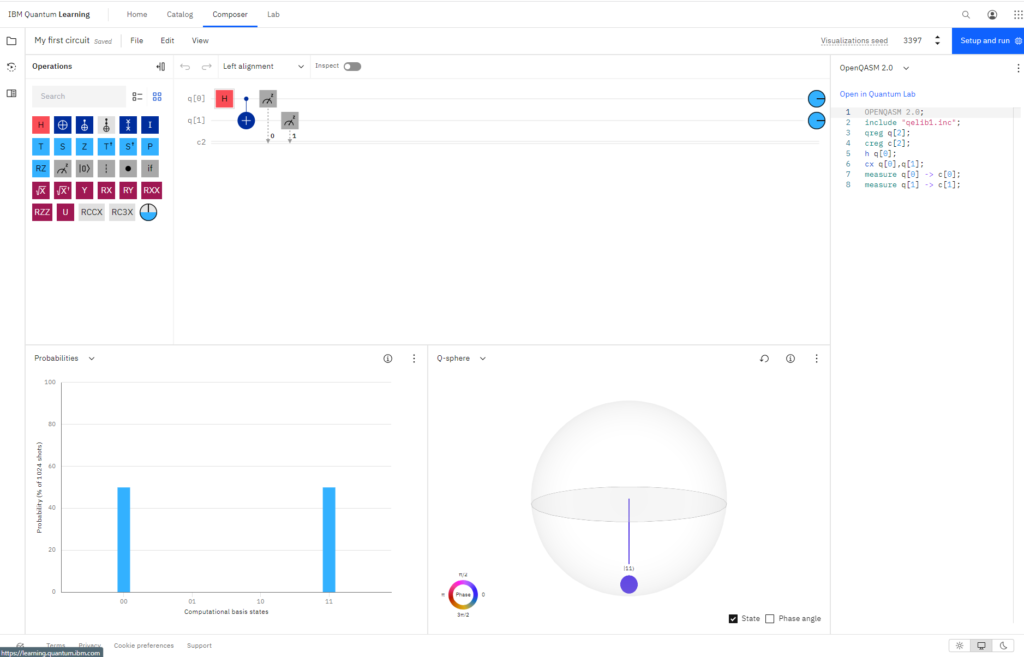
各機能説明は以下です。
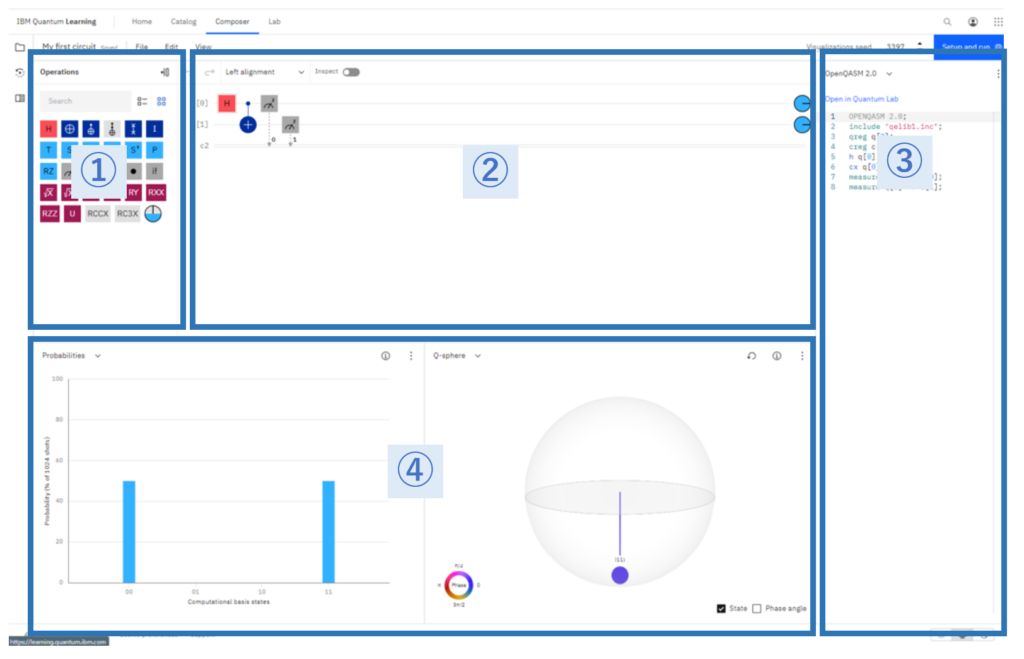
- Operations catalog
量子ビットに対する操作がブロックとして並んでおりこのブロックを②の回路エディターにドラッグ&ドロップすることで簡単に量子プログラミングができます。 - Graphical circuit editor
量子ビットに対する操作を視覚的に表現しています。五線譜のように線が並んでいますがこれらひとつひとつが量子ビットを表しています。一番下の二重線は従来のビットを表しています。この線上にブロックを置くことでその量子ビットへの操作を指定できます。これまた五線譜のように、処理は左から順番に実行されます。 - Code editor
量子プログラミング言語などを使ってコーディングができます。 - Visualizations
量子ビットの状態を視覚化してくれます。左側は出力される値の確率、右側はブロッホ球と呼ばれる量子ビットの状態の表現の一種を表しています。

プログラムの作成をしてみましょう。
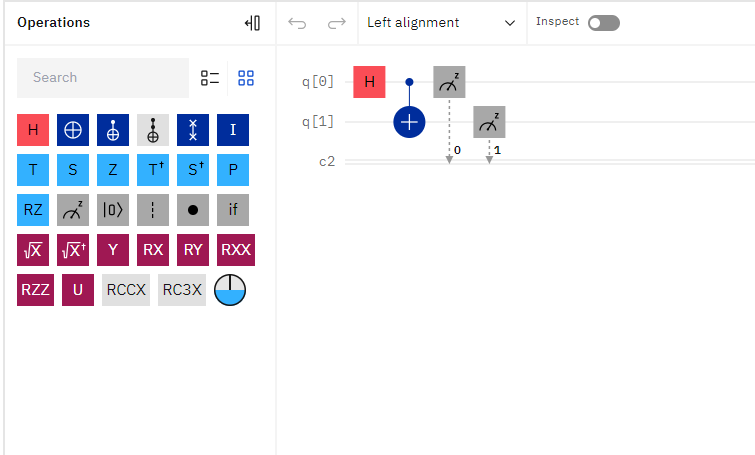
左の Operations から Graphical circuit editor にドラッグ&ドロップでこの様に持っていきましょう。
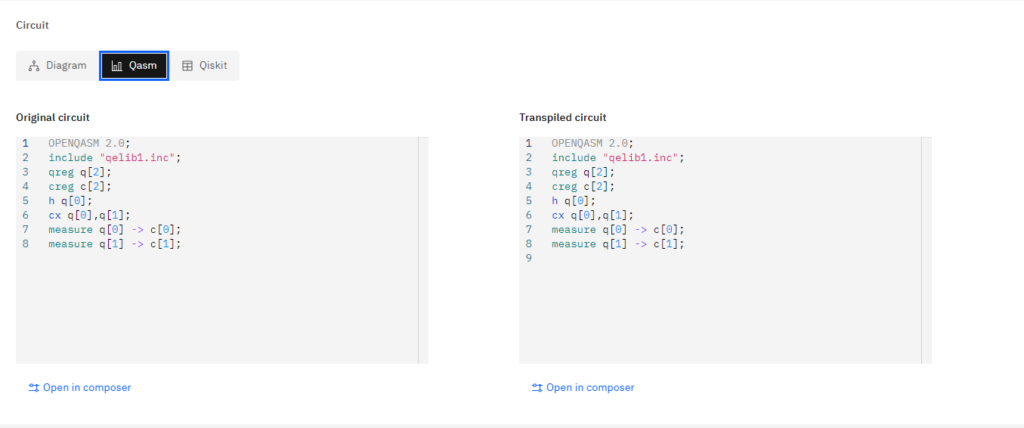
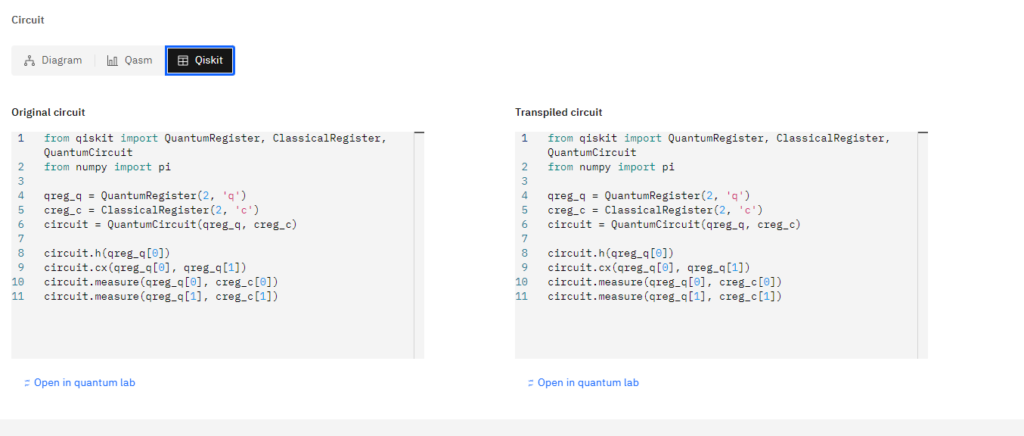
コードとしては以下の様になります。
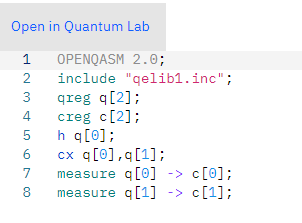

プログラムを実行してみましょう!
Quantum Composerではプログラムを簡単に実行できます。右上にある青い「Setup and run」と書かれたボタンを実行しましょう。
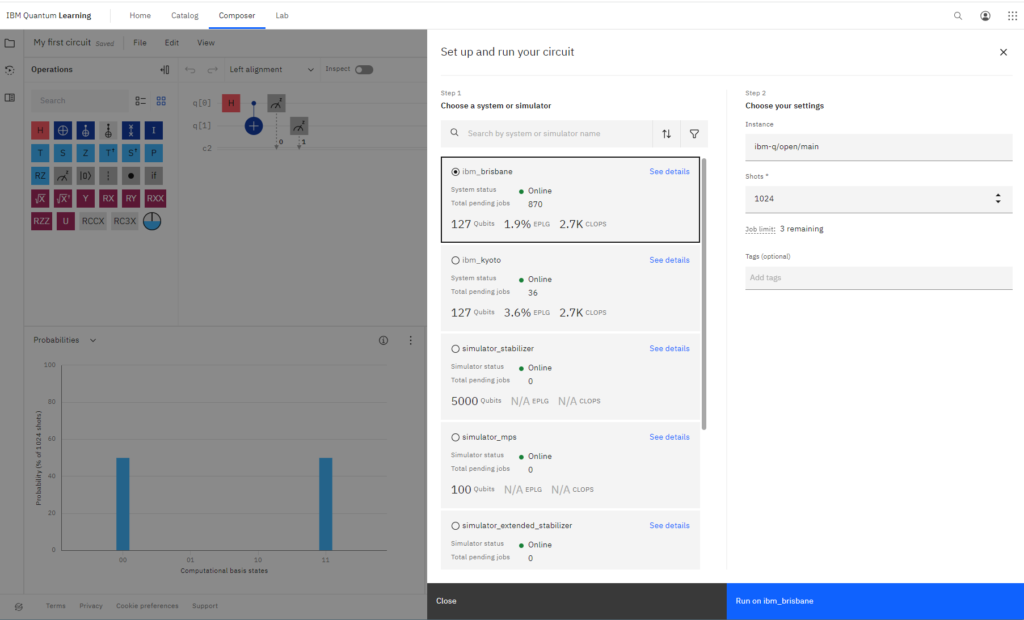
「Choose a system or simulator」と、選択できる量子コンピュータの実機やシミュレーターが並んでいます。「simularor」と書かれていないものはすべて実機になります。以下だと日本の京都の実機です。
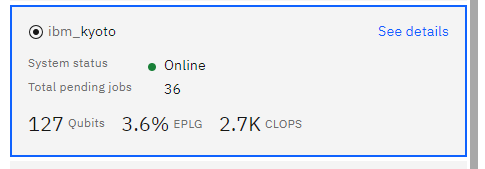
それぞれの実機についていろいろな情報が書かれていますが、実行前に注意してみるべき場所は「Total pending jobs」の部分です。ここには現在保留されているプログラムの数が書かれています。上の画像では「36」と書かれていますので36個のプログラムが実行が待ち行列に入っていることになります。そのためなるべく数値が低いものを選ぶとよいでしょう。
システムを選んだら右側にある「Shots」の数値を変えて実行回数を調整しましょう。量子コンピュータの出力は確率的です。なので何回も実行して出力される値の分布を見るのが一般的です。今回はShotsの値を「1024」にして1024回実行するようにしましょう。

さて!実行状況を確認しましょう。
以下の部分を選択しましょう。
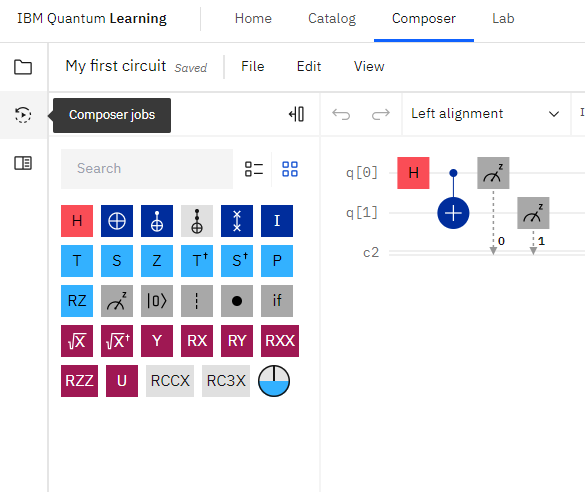
実行結果は左側のツールバーから確認できます。
待ち行列やステータスは以下の様に確認できます。ここでは「19分の待ち行列にはいっています」と表示されています。
またJobs の から jsonのダウンロードもできます。
cnkk0s3tpj7000841bz0-info.json のようなファイルを zip形式でダウンロードできます。
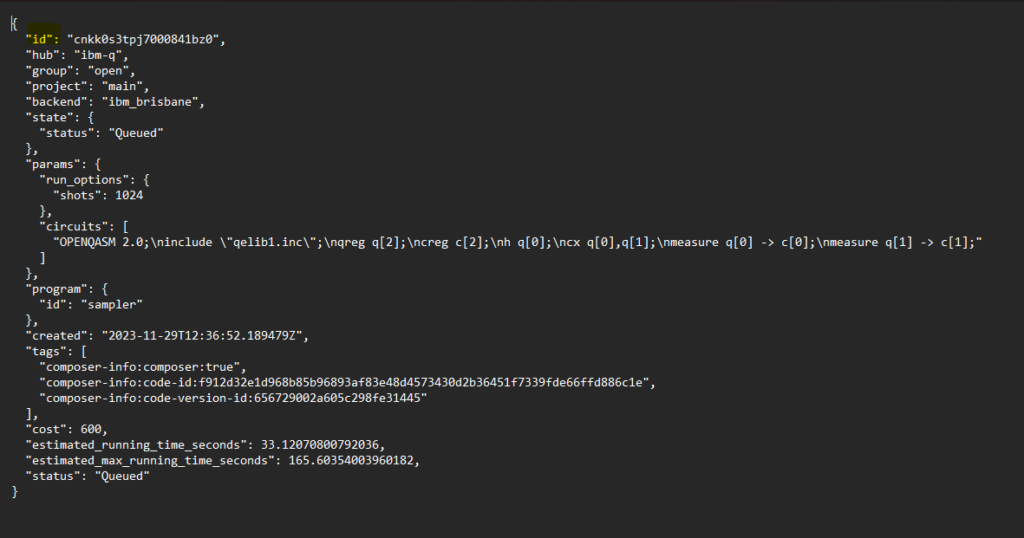

実行結果が出ました。Jobsで詳細が確認できます。
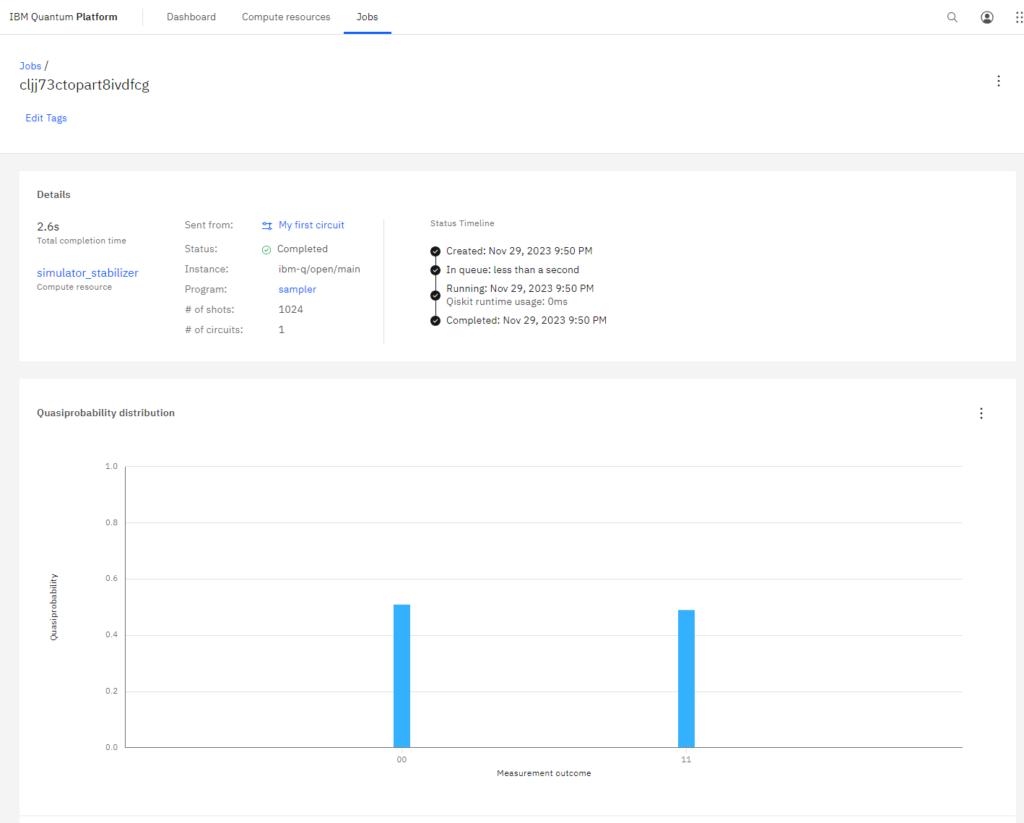
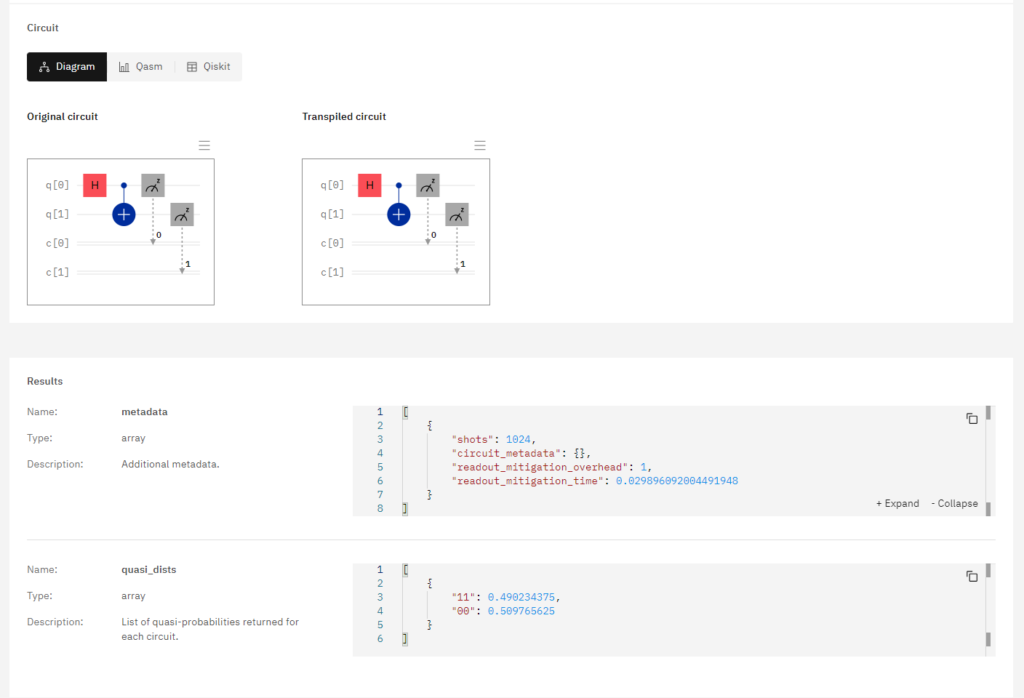
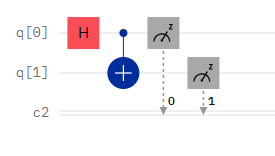
「q[0]」とは量子ビットで、「c2」とは古典ビット(従来のビット)を表しています。「q[0]」は初期状態で「100%の確率で0」の状態です。なので「H」(アダマールゲート)がなければ必ず0を出力するプログラムになります。

Hゲートは、アダマールゲートと呼ばれるもので、量子重ね合わせ状態を作ることができる重要なゲートです。|0⟩が、|0⟩と|1⟩の重ね合わせ状態になります。
(補足説明)
量子ビットは|0⟩と|1⟩の2つのエネルギーレベルで構成されるシステムです。|0⟩状態は2つのエネルギーレベルのうち低い方であるため、基底状態と呼ばれることもあります。|0⟩と|1⟩を合わせると「標準基底ベクトル」を作ることができます。ベクトルと同様にそれらは方向と大きさを持ちます。基底ベクトルを定義することは、線形代数から拝借したものです。一度これらのベクトルを定義すれば、基底ベクトルの線形結合から他のベクトルを構築できるというのが基本的な考え方です。
さらに量子ビットは「位相」をもちます。これは重ね合わせが複雑になることが原因です。これらの重なり具合を表現するために,基底状態の前にaやbのような係数を次のように入れます。

基底は|0⟩と|1⟩で表され、それらの線形結合a|0⟩+b|1⟩は単一量子ビットの状態を表します。係数aとbは実数に限らず、虚数や複素数もとり得るため、量子ビットを視覚化するには「ブロッホ球」と呼ばれる特別なツールが必要になります。ブロッホ球は半径1の球であり、その表面上の点は量子ビットの状態を表します。地球の表面上の点を記述するために経度と緯度を使用するように、ブロッホ球は角度を使って量子ビットの状態を記述することができます。この表現は、複素係数を含む量子ビット状態をブロッホ球の表面上の点として表現するようにしています。x、y、z軸に沿ったブロッホ球の表面上の点は以下に説明する特別な状態に対応します。
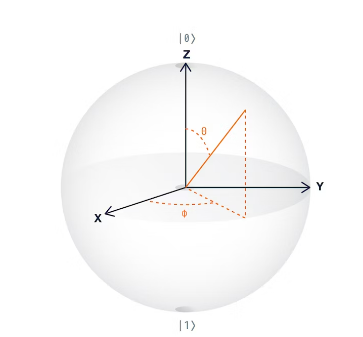
量子ビットの状態は、上の画像のオレンジ色の線で示されています。この図では球の頂点の状態は|0⟩を表し、球の底の状態は|1⟩を表します。量子ビットが|0⟩と|1⟩の重ね合わせをとると、ブロッホベクトルは|0⟩と|1⟩の間のどこかを指します。